OO第一单元总结 - 表达式展开

题目回顾：

第一次作业：实现含有加，减，乘，幂次，数字，未知数的单层括号的表达式展开

第二次作业：增加了三角函数，自定义函数与递推函数，允许多层括号嵌套

第三次作业：增加了求导操作，增加了普通自定义函数

程序整体架构

类图

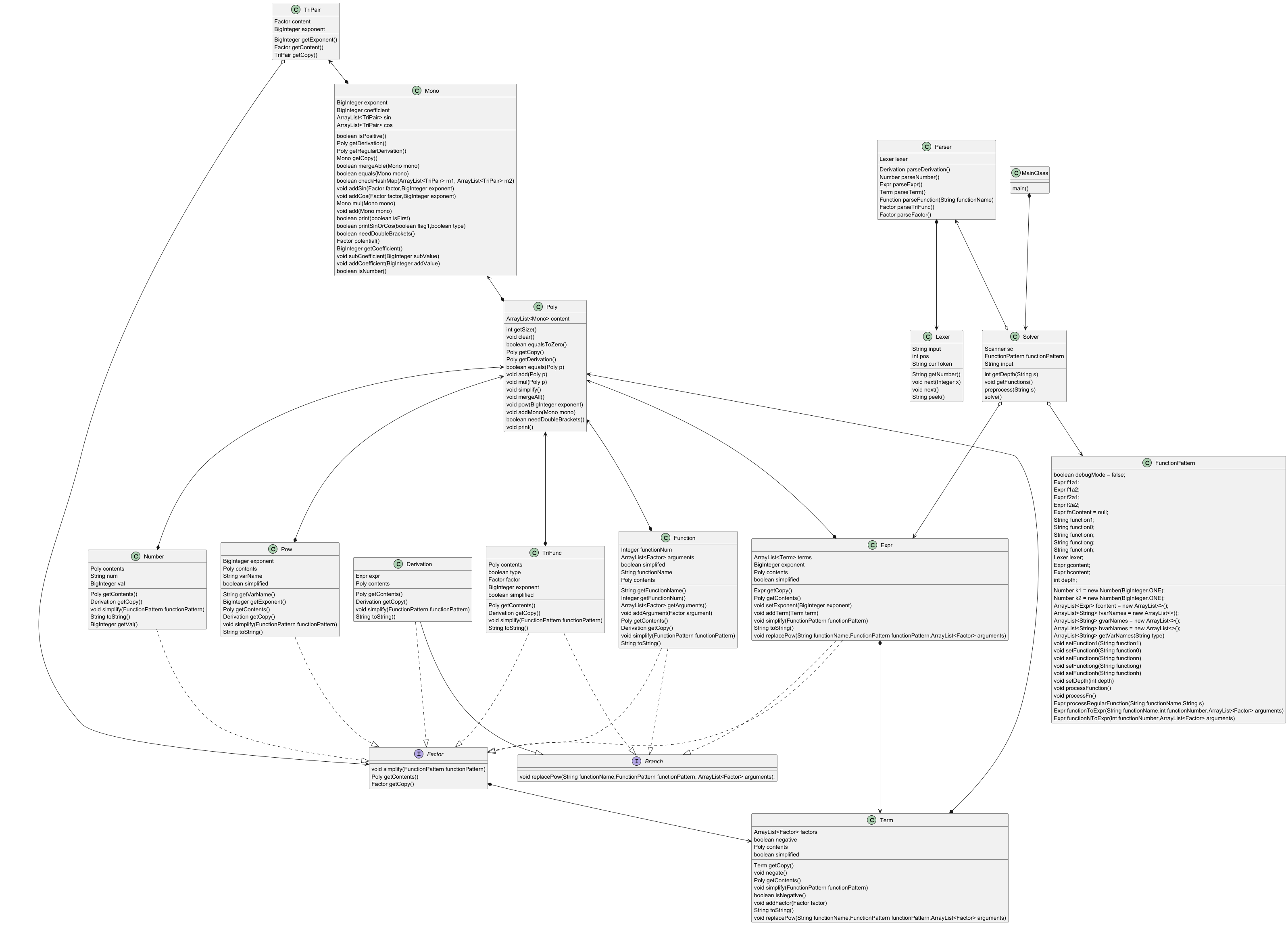
优点：使用两个接口，使架构清晰，方便统一管理，易于迭代。

缺点：其实写的时候感觉很舒服，没有感觉到有明显缺点（）

架构介绍

Class:
MainClass:程序入口
Solver:负责预处理输入数据，进行整个程序流程
Lexer:词法分析器
Parser:语法分析器
Expr:表达式类
Term:项类
Number:数字因子类
Pow:幂函数因子类
TriFunc:三角函数因子类
Function:函数因子类
Derivation:导数因子类
FunctionPattern:函数信息类，负责管理整个函数展开功能
TriPair:自己写的Pair，存储一个三角函数内部的因子和幂次
Poly:多项式类，用于储存数学表达式化简后的具体内容
Mono:单项式类，Poly是Mono的组合
Interface:
Factor:因子接口，负责管理各个种类的因子
	包含:Expr,Number,Pow,TriFunc,Function,Derivation
Branch:枝接口，负责管理表达式树上的非叶子节点——用于简化递归遍历表达式树的实现，增强可迭代性
	包含:Expr,TriFunc,Function,Derivation

性能度量分析

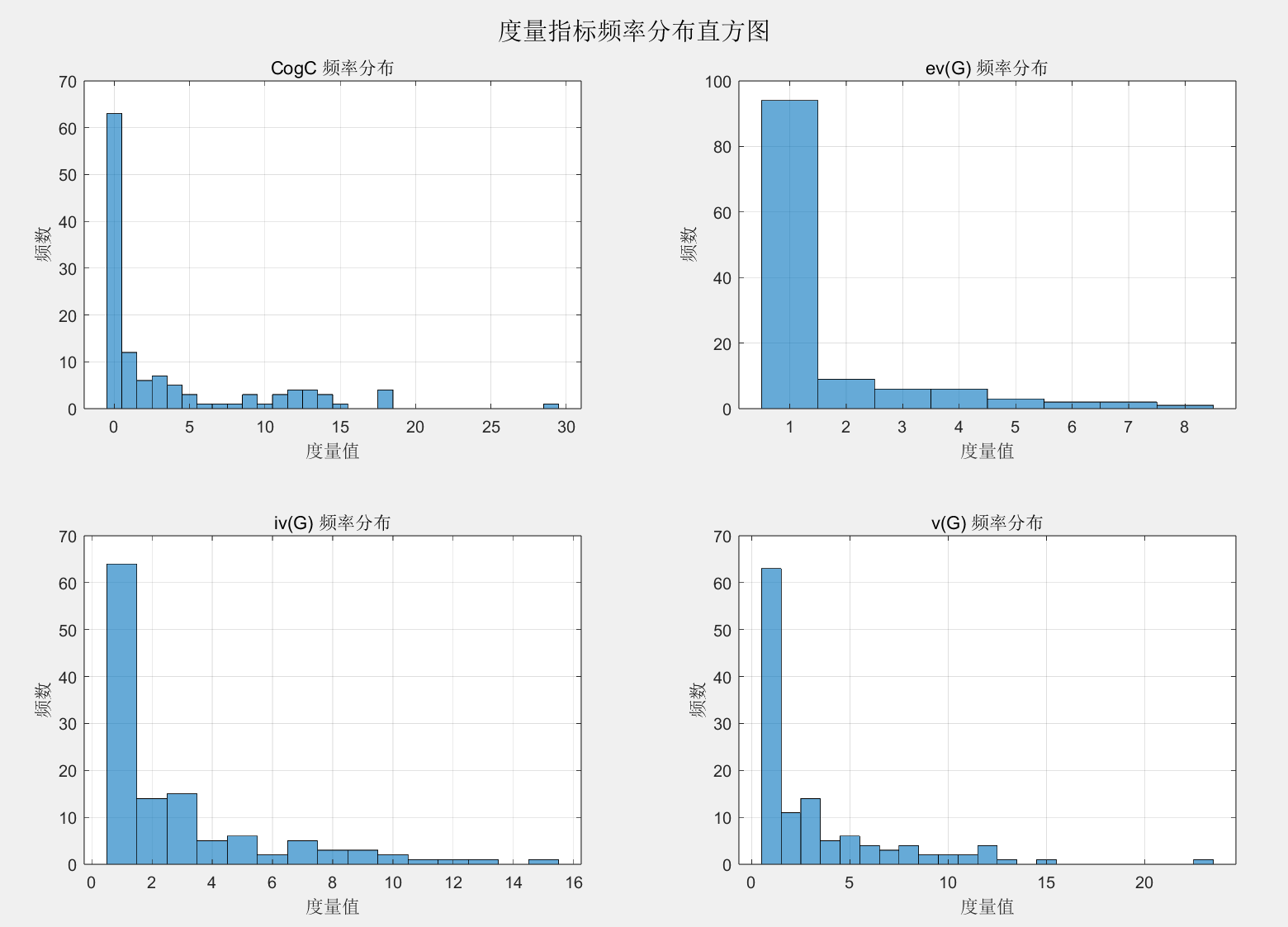
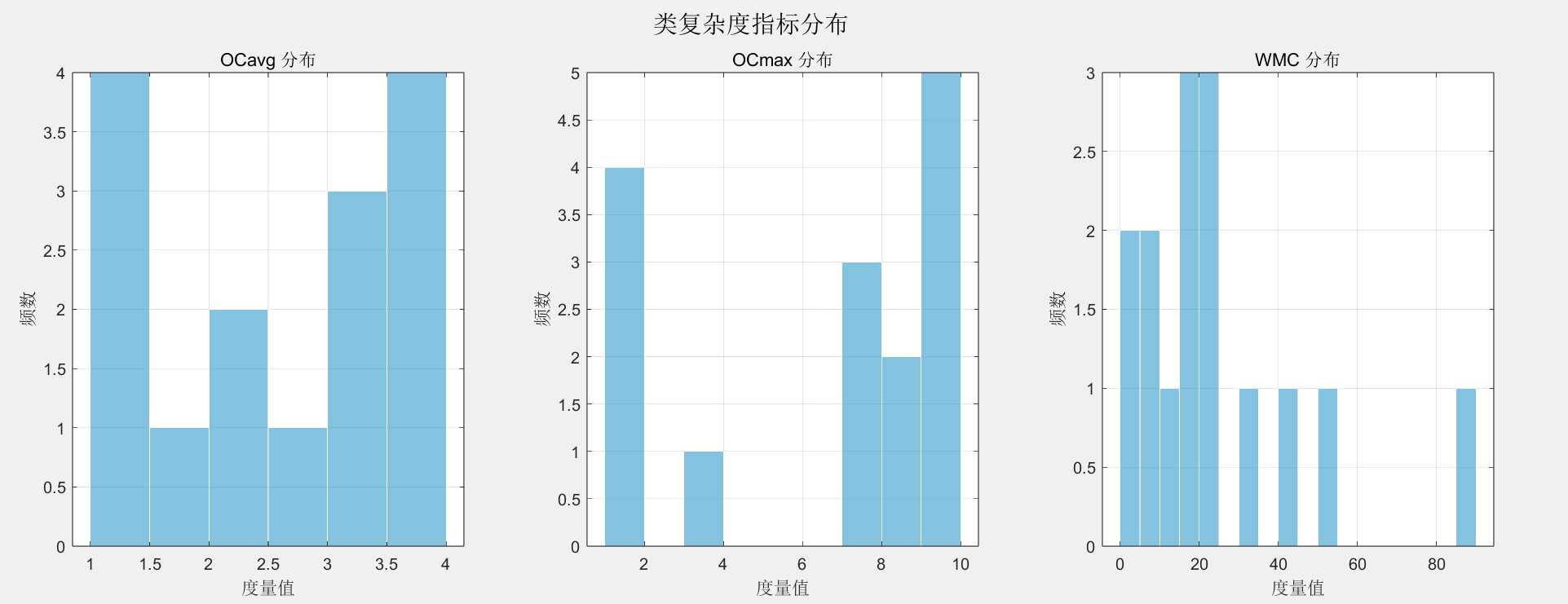
Project	V(G)_avg	V(G)_tot
Unit1	3.36	413

架构设计体验

第一次作业：

第一次作业时，由于没有看OO的公众号文章，我没有选取用的比较广的 Mono 和 Poly 的架构，而是自己设计了基于继承的架构。

具体来说，在我们表达式的展开化简部分，我们要把各个数学单位的展开后的值存储起来，并为其加，乘，幂的运算专门写方法。在第一次作业通过一个 HashMap<BigInteger,BigInteger> content ，来存储系数指数的对应关系，已经足够使用。考虑到所有的数学单位都有这一个成员，并需要运算方法，我选择了使用继承结构，将各个数学单位归为数学表达式类 Expression 的子类中，在 Expression 中写入相关运算方法和成员。

第一次作业最终的架构整体流程则为，首先对输入进行预处理，去除空白字符，前缀零，对于一些连续的加减符号进行合并，然后利用 parser 对表达式进行递归下降解析，建立树状结构。接下来二次扫描，为每一个数学单位写 simpilfy 方法，扫描过程中自上向下递归进行遍历，每一个节点先调用儿子的 simplify 方法，接下来使用 Expression 的加，乘等方法直接对儿子进行运算，得到自己的 content ，最终得到结果。

重构:

由于各个类的共性在于其拥有一个共同的成员，而我们设计的父类的运算方法也在于这些成员之间的运算方法。所以实际上将这一个共同的成员专门建类，并在这个类中设计运算方法更加合适。

在第一次作业迭代到第二次作业时，之前架构的缺陷使迭代难以进行，故我对第一次作业的代码进行了重构。重构的点主要在于删除了继承关系，而将 HashMap<BigInteger,BigInteger> content 封装了起来，并将其分为了两层，一层是表示单项式的 Poly ，一层是表示单项式的 Mono 。

Poly 由 ArrayList<Mono> 组成。Mono 内部有相应的加，乘，的方法，而 Poly 拥有加，乘，幂次和合并内部 Mono 的方法（即寻找是否内部由指数相同的 Mono ，将他们合并为一项）。这样的架构社计更为合理与清晰。

第二次作业

第二次作业引入了三角函数和函数，迭代难度很大，以下是对于这两个问题的解决策略。

三角函数带来的计算问题

继续沿用上一次作业的 Mono 和 Poly 方法，由于本次作业不能再表述为 $\sum\limits_{i=1}^{n}a_ix^b$ 的形式，可以这样来表述：
$$
Poly = \sum\limits_{i-1}^nMono = \sum\limits_{i=1}^{n}a_ix^{b_i}(\prod_{j=1}^{n_1}sin(\alpha_j)^{\beta_j})(\prod_{k=1}^{n_2} cos(\gamma_k)^{\aleph _k})
$$
对于 $sin$ 和 $cos$ 有关的内容，我们可以用两个 HashMap<Factor, Integer> 来解决。

注：由于这里的 HashMap 其实只是利用了他能存一对值的特性，而没有用到他的 Map 特性，我在后续迭代中自己写了 TriPair ，并使用了 ArrayList 替代 HashMap。

通过重写 Mono 中加，乘，幂次的方法，就可以解决三角函数的引入带来的计算问题。而 Poly 中的方法不需要大改，因为其只是 Mono 方法的组合。

函数部分

核心思路：

建立FunctionPattern类对函数进行预处理
通过对幂函数的替换，实现当 $n=0,1$ 时，函数因子对表达式因子的转换方法
通过递归调用函数转换方法来解决 $n$ 较大时的函数问题。

具体实现

我们在预处理时，通过建立一个 FunctionPattern 类，来解析并记录$f_0$ ,$f_1$ 的内容，以及 $f_n$ 的构造方法。

细节来说，对于 $f_0$ 和 $f_1$ 的解析我们可以使用现成的 parseExpr，而 $f_n$ 的构造方法我们要记录两个用来乘的系数，利用 parseFactor 来解析两个/四个参数因子，以及可能存在的，需要额外加上的表达式。即我们需要解析下面列出的内容。

1
2
3

f{n}(x,y) = k1*f{n-1}(f1a1,f1a2) + k2*f{n-2}(f2a1,f2a2) + fnContent
f{0}(x,y) = f0Content
f{1}(x,y) = f1Content

在 FunctionPattern类中，我们需要实现一个关键方法 Expr functionToExpr(Integer functionNum, ArrayList<Factor> arguments) ，通过调用该方法，可以实现传入一个函数因子的序号以及其参数列表，返回一个处理完毕的表达式的功能。

关于其具体实现，可以分为以下两种情况：

如果 functionNumer 为 1 或 0 ，则对f1Content或 f1Content 做一个深拷贝，复制其所有的值，而不是复制其指针（如果不这么做的话，每次调用都会破坏 f0Content 或 f1Content）

遍历深拷贝后的表达式，如果在某一层级，发现他的一个儿子是一个幂函数类型的因子，则对这个幂函数的变量名对应的参数做一个深拷贝，将这个 Factor 类型的对象在外面套一层 Expr ，在套上的这层 Expr 上面，加上被替换的幂函数的因子。

这里的替换一定要使用 ArrayList 的 set(i,Factor) 这样的方法，可以防止被重复替换。
如果 functionNumber 大于 1，则首先调用本方法，解析出 f{n-1}(arguments) 和 f{n-2}(arguments) 对应的两个表达式，然后已知 k1，k2 ，fnContent，构造出对应的表达式并返回即可。

注意： fnContent 也要进行深拷贝并进行遍历替换

关于这个类的使用，我在 Solver 中提前解析了该类，然后把他作为了 simplify 方法的工具参数，递归往下传，如果看到了函数因子就使用这个工具。

这样子差不多就能解决函数问题了，关于对于幂函数的遍历替换和深拷贝部分，则需要在Expr,Term等等诸多类中完成其方法，才能实现完整的深拷贝和遍历替换。

对于函数中引入的多变量xy有关的处理，我们注意到，我们只需在解析时知道是多变量，而不需要实际利用多变量进行任何的运算操作。

可以直接在幂函数类中增加一个 String varName 成员，记录其名称，在处理函数时对多变量进行处理。而在计算时，我们把幂函数仍作为 $x^n$ 来看没有任何影响。这样子多变量就轻松解决了。

第三次作业

第三次作业迭代增加了更多自定义函数，以及求导操作，难度较小。

求导操作的引入

对于求导操作，只需增加导数因子及相应的解析方式。在Mono中增加Mono的求导方法，并利用 Mono 的求导方法拼出 Poly 的求导方法。Mono 和 Poly 其他内容我们无需改动。

假设新的迭代情景

我们假设引入了虚数单位 i ，关于我的程序事实上不需要过多的改动。

增加虚数因子

需要增加虚数因子有关的词法解析和语法解析，并增加虚数因子类。以及关于虚数因子的输出逻辑。

增加虚数有关运算

在Mono中增加一个关于虚数flag的成员，同时增加 Mono乘法关于虚数的相关逻辑，和对于加法合并判断时的判断逻辑。

程序 bug 分析

本人的程序在第一单元中被互测TLE 攻击成功过一次。追数据开放后才发现， hacker 使用嵌套极深（约20层）的 sin 嵌套成功让我程序 TLE 卡炸了。

bug 的主要原因在于，本人的 Mono 项内部存储了 sin 与 cos 内部的 Factor ，而本人在深拷贝的过程中，对于 Factor 的 Poly 进行了深拷贝，而 Poly 又对 Mono 进行深拷贝，Mono 又对其所有属性进行了深拷贝。这个行为逻辑上没有问题，但是 Mono 的深拷贝同样拷贝了它的 Factor ，接下来会不断嵌套下去，导致每一次拷贝的时间复杂度都是基于嵌套层数的指数级函数，故会被深层次嵌套进行 TLE 攻击。但是事实上 Mono 对于其因子的深拷贝时不必要的，因为深拷贝的主要目的是防止对象被其他管理者进行预料之外的修改，但是 Mono 不会去修改 Factor 的任何内容，故在 bug 修复时只需删掉 Mono 对于 Factor 的深拷贝调用即可。

事实上这个 bug 较为隐蔽。由于缺乏经验，在深拷贝时我严格按照深拷贝时的相关逻辑以防出错，但是正是因为这个，导致逻辑上正确，却在性能上吃亏。

复杂度分析

	行复杂度	圈复杂度
出现了bug的方法	1	0
未出现bug的方法	1	0

本方法在修改前后的复杂度完全一致且均很低，从这里无法得到结论。

发现别人 bug 采取的策略

首先最有效但是效率较低的方法当然是评测机轰炸了！通过数据生成器，按照文法逻辑递归生成较为全面的数据。数据生成器要保证数据要有一定的复杂度，能够随机出来大多数情况，同时又要控制数据的规模不能过大，以防评测机无法评测（时间超时）。

其次是手动构造极端样例，例如多层 sin 嵌套攻击一些 TLE 的 bug ，以及 (x)^8^ 嵌套这种 bug，这种数据一般无法用评测机roll出来，手动构造较为合适。

我 hack 时并无阅读别人代码，通过阅读代码的方式攻击效率过低，且很难有收益，不如评测机（）。

优化分析

每增加一行代码有可能引入潜在的bug，因此我只进行最易进行的优化，将 $asin(\delta)^2+bcos(\delta)^2$ 优化为了 $(a-b)sin(\delta)^2+b$ ，并消掉其中的含零项。这个优化可以通过为 Poly 重写 equals 方法，来对三角函数内部因子进行比较，并在 Poly 进行加法时尝试优化。

同时，对于同类项的合并优化也较为简单，同样是重写 equals 方法，在相加时合并，这里不多赘述。

本人的优化仍然能保证程序的简洁性。关键在于将优化所使用的代码封装起来，并将功能逐级拆分。例如，在进行优化时有一个前提条件是两个 Mono 都为 $asin/cos(x)^2$ 的形式，我在 Mono 中设计了 potential 方法，表示这一个 Mono 具有这样的特性（即拥有继续优化的潜力），这样就增加了优化代码的可读性，优化的功能调用时也只用增加一行函数即可。

心得体会

对于架构的体会

第一次作业是我完全理解了架构设计对于面向对象项目的重要性，一个好的架构能够增强代码的可读性和可迭代性，同时使自己编程使有一个清晰的思路，清楚的明白自己在做什么，要做什么。

一个好的架构，应当将功能封装独立起来，满足高内聚低耦合的特征。同时要能够提取共性特征，建立适当的接口，以方便统一管理，降低代码的复杂度，减少重复代码，方便迭代。

对于测试的体会

一个自动化的，可复用的自动测试工具在项目的开发中至关重要。在优化性能，增量开发，修复bug的过程中，很有可能会对之前代码的正确性造成影响。在代码迭代的时候，一个好的评测系统可以帮助自己快速定位bug。

本次作业我直接使用互测用于攻击别人的评测机来进行高强度自测，在自测后我的代码没有任何逻辑上的错误，只有性能上的缺陷。

对于评测机以及大模型使用的一些小心得

本人的评测机主要分为三部分，数据生成器，对拍器，以及整合脚本。数据生成器将批量的数据生成到一个文件夹下，对拍器读取这个文件夹的数据，将标程和待测jar文件的输出数据也放到这个文件夹中。

评测机的数据生成器和对拍器的分离我认为是一个非常重要的设计，通过分离的设计，可以选择使用数据生成器的数据还是使用文件夹中本来就有的数据。

同时，评测机的对拍器（spj）部分逻辑较为简单，我们可以把这些任务丢给大模型来做，自己完成逻辑复杂的数据生成器部分。这样能够提升我们的很多工作效率。

使用大模型时，最重要的是能够给出明确清晰的提示词，我将我制作spj的提示词放在下面，可供参考。

当然，我们使用时要严格按照课程的制度，在禁止使用的部分（如作业本体）不要用大模型。

未来方向

希望课程组优化课程网站排版，尤其是形式化表述的部分，不要用不加任何修饰的普通文字堆成一坨，观感很差。
希望难度提升更加平滑，本次作业第一单元hw1到hw2的难度提升很大，而hw2到hw3的难度提升较小，我身边不乏写hw2用了十小时以上，写hw3只用了三个小时的同学。可以将求导和三角函数操作放在hw2，自定义函数的两个部分整合一起放在hw3。